Zapraszamy naszych uczniów do rozwijania zainteresowań matematycznych. Na każdy miesiąc publikujemy po 4 zadania dla poszczególnych klas. Pogłówkujcie 😀

Maj

Klasa 4

1. Ciastko marcepanowe jest o 20 gr droższe od ciastka czekoladowego. Za 3 ciastka czekoladowe i 2 marcepanowe zapłacono 8 zł 35 gr. Ile kosztuje ciastko czekoladowe?
2. Rozszyfruj zagadkę: jaka liczba powinna być w okienku z niebieskim rombem (patrz rysunek)?
   

3. Paulina robiła kwiatki z bibuły. Wykonywała na  przemian: 4 różowe kwiatki, potem dwa żółte. Jaką część wykonanych przez nią kwiatków stanowią  kwiaty żółte, jeśli zrobiła 24 kwiatki?
4. W pewnym mieście ulica Czekoladowa jest równoległa do ulicy Słodkiej i prostopadła do ulicy Ciasteczkowej. Ulica Słodka jest prostopadła do ulicy Pyzatej, która jest prostopadła do ulicy Pysznej, która z kolei jest równoległa do ulicy Batonikowej. Która ulica jest równoległa do ulicy Ciasteczkowej?

Klasa 5

1. Nit i dwa gwoździe ważą razem 11,3 g, a dwa nity i jeden gwóźdź ważą razem 9,1 g. Ile waży jeden nit, a ile jeden gwóźdź?
2. W pewnej szkole podstawowej 35% dzieci to jedynacy. 46% dzieci ma siostrę, a 47% – brata. Ile procent dzieci uczęszczających do tej szkoły ma siostrę i brata?
3. Znajdź cztery takie liczby, że każda następna jest większa o 2,15 od poprzedniej, a ich suma wynosi 16.
4. Każdej literze przyporządkowano inna liczbę podana w tabelce.
   

W zapisie K _ _ _ K napisz zamiast _ litery tak, aby otrzymany wyraz był rzeczownikiem, a iloczyn liczb odpowiadających poszczególnym jego literom był równy 0, 000024.

Klasa 6

1. Pole powierzchni sześcianu wynosi 150 cm². O ile procent wzrośnie pole powierzchni tego sześcianu, jeżeli długość krawędzi zwiększymy o 1 cm?
2. Pewien hodowca sprzedawał chomiki i kanarki. Wystawił na sprzedaż łącznie 36 sztuk zwierzaków. Oblicz, ile było kanarków, a ile chomików, jeżeli miały one w sumie 100 nóg.
3. Prostokąt i kwadrat mają taką samą powierzchnię równą 36 cm². Długość jednego boku prostokąta stanowi jedną trzecią długości boku kwadratu. Oblicz obwód prostokąta.
4. Z sześciennego akwarium o wysokości 80 cm wypełnionego całkowicie, przelano wodę do większego akwarium, którego podstawa jest prostokątem o wymiarach 6 dm i 1 m. Woda zajęła większego akwarium. Oblicz wysokość tego akwarium. Ile litrów wody trzeba jeszcze dolać, aby zapełnić to akwarium?

Klasa 7

1. W równoległoboku jedna z podstaw ma 12 cm, a wysokość opuszczona na tę podstawę 5 cm.
   Jaka jest długość drugiej podstawy, jeżeli wysokość opuszczona na tę podstawę ma długość 6 cm?
2. Boisko piłkarskie ma wymiary 76m x 110m. Jeżeli worek trawy wystarczy na obsianie 5 arów, to ile takich worków trzeba będzie zakupić, by obsiać całe boisko?
3. Wysokość trójkąta jest 3 razy dłuższa od boku, na który jest opuszczona i wynosi 12 cm. Jakie pole ma ten trójkąt?
4. Obwód trapezu równoramiennego wynosi 28 cm, każde ramię ma długość 5 cm, a wysokość ma długość 4 cm. Oblicz pole tego trapezu.

Klasa 8

1. Wykaż, że liczba m³ – m jest podzielna przez 6.
   Twierdzenie 1: Dla dowolnej liczby naturalnej n liczba 10ⁿ – 1 jest podzielna przez 9.
   Twierdzenie 2: Niech n będzie liczbą naturalną. Wówczas liczba 10ⁿ – 1 jest podzielna przez 11 wtedy i tylko wtedy gdy n jest liczbą parzystą.
2. Korzystając z twierdzenia wykaż, że liczba (10¹⁵ – 1) : 9 jest naturalna.
3. Korzystając z twierdzenia wykaż, że liczba (10¹² – 1) : 11 jest naturalna.
4. Rozstrzygnij, czy liczba (10³⁷ – 1) : 11  jest naturalna.

Kwiecień

Klasa 4

1. Dwa automaty miały wyprodukować 30 000 opakowań do kefiru. Pracowały razem przez 3 dni po 8 godzin dziennie robiąc w ciągu godziny 450 opakowań. Po trzech dniach jeden z automatów się popsuł. Ile dni przez 8 godzin dziennie musi jeszcze pracować drugi automat, jeśli w ciągu godziny wyrabia on 240 opakowań? Zapisz obliczenia.
2. W skład zespołu muzycznego wchodzą cztery dziewczynki: Sandra, Felicja, Gabrysia i Paulina. Grają one na skrzypcach, flecie, gitarze i pianinie. Żadna z dziewcząt nie gra na instrumencie, który zaczyna się na pierwszą literę jej imienia. Sandra mieszka razem z pianistką. Paulina i grająca na flecie są najlepszymi przyjaciółkami. Gabrysia gra na skrzypcach pożyczonych od Sandry. Która z dziewcząt gra na pianinie?
3. Poniższe liczby zostały zapisane zgodnie z pewną regułą. Odkryj ją i podaj jaka będzie następna liczba?
   1; 2; 4; 7; 11; 16; 22; ?
4. Siedem patyków, każdy o długości 14 cm, ułożono jak na rysunku na długości 80 cm. Każdy z odcinków oznaczonych znakiem zapytania ma taką samą długość. Jaką?

Klasa 5

1. Janek wypił ⅙ szklanki wody i dolał soku. Następnie wypił ⅓ szklanki wody z sokiem i dolał soku. Potem wypił ½ szklanki wody z sokiem i znów dolał soku. Na końcu wypił całą szklankę wody z sokiem. Czego wypił więcej – wody czy soku, jeżeli za każdym razem dolewał tyle soku, aby szklanka była pełna?
2. Dąb ma 22 lata, a sosna 6 lat. Za ile lat dąb będzie 3 razy starszy od sosny?
3. Pitagoras, matematyk grecki, który żył w VI w. p.n.e. zapytany o liczbę swoich uczniów, odpowiedział: „Połowa moich uczniów uczy się matematyki, czwarta część przyrody, siódma część milczenia, resztę stanowią trzy kobiety”. Ilu uczniów miał Pitagoras?
4. Znajdź liczbę dwucyfrową, w której różnica cyfry dziesiątek i cyfry jedności wynosi 6, a cyfra jedności stanowi ¼ cyfry dziesiątek.

Klasa 6

1. Znajdź liczby, które przy dzieleniu przez 2, 3, 4, 5 dają tą samą resztę.
2. Mama sporządzała 4% roztwór soli kuchennej do kiszenia ogórków. Wsypała do naczynia 0,15 kg soli i wlała odpowiednią ilość wody. Ile wody wlała mama?
3. Z Opola o godzinie 12.00 wyjeżdża samochód ciężarowy z prędkością 65 km/h, 45 minut później w tym samym kierunku wyjeżdża samochód osobowy z prędkością 80 km/h. O której godzinie samochód osobowy wyprzedzi samochód ciężarowy?
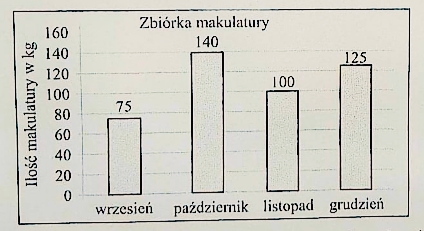
4. Diagram przedstawia wyniki zbiórki makulatury w pewnej szkole. Ile makulatury powinni zebrać uczniowie w styczniu, aby średnia wzrosła o 10 kg?
   

Klasa 7

1. Stefan hoduje kanarki. Na pytanie ile ich ma odpowiedział “¾ tego, co mam, plus ¾ kanarka”. Ile kanarków ma Stefan?
2. Piekarz sprzedaje świeże bułeczki po 40 groszy za sztukę. Przy zakupie ponad 10 sztuk za każdą następną płaci się tylko 30 groszy. Ile bułeczek można kupić za 10 złotych?
3. Załogę promu kosmicznego tworzy sześciu astronautów. Średnia wieku członków załogi bez kapitana jest równa 36 lat, a z kapitanem jest o rok wyższa. Ile lat ma kapitan?
4. – Dziadku, ile masz lat?
   – Rok temu byłem dwa razy starszy od cioci Agaty.
   – A ile lat ma ciocia Agata?
   – Dwa lata temu miała trzy razy tyle, ile lat miała wtedy twoja kuzynka Kasia.
   – A ile lat ma Kasia?
   – Kasia jest o 66 lat młodsza ode mnie.
   – Aha, to znaczy, że ty dziadku masz teraz…
   No właśnie – ile lat ma dziadek?

Klasa 8

1. Suma trzech kolejnych liczb nieparzystych jest równa 51. Znajdź te liczby.
2. Bilet wstępu dla osób dorosłych do ogrodu botanicznego kosztuje 10 zł. Dzieci płacą 70% tej ceny. W sobotę ogród botaniczny odwiedziło 80 osób, płacąc za bilety łącznie 665 zł. Ile dzieci i ilu dorosłych odwiedziło w tę sobotę ogród botaniczny?
3. Drużyna piłki ręcznej składa się z 7 zawodników. Średni wiek zawodnika tej drużyny jest równy 25 lat. Podczas meczu jeden z zawodników tej drużyny musiał opuścić boisko. Średni wiek pozostałych zawodników był równy 24 lata. Ile lat miał zawodnik, który opuścił boisko?
4. W trapezie prostokątnym ABCD kąt rozwarty BCD ma miarę 120°, a kąt zawarty między przekątną AC i podstawą AB ma miarę 30°. Wykonaj rysunek pomocniczy i wykaż, że trójkąt ABC jest prostokątny.

Marzec

Klasa 4

1. W biegu na 120 m przez płotki pokonuje się 10 płotków, które ustawione są tak, że odległość pierwszego płotka od startu wynosi 13 m, a ostatniego od mety 17 m. Ile wynosi odległość między kolejnymi płotkami, jeśli rozmieszczone są w jednakowych odstępach?
2. W pewnym miesiącu trzy czwartki wypadły w dni parzyste. Jaki dzień tygodnia jest 18 dnia tego miesiąca?
3. Suma trzech liczb wynosi 783. Druga liczba jest 2 razy większa od pierwszej, a trzecia liczba jest 3 razy większa od drugiej. Ile wynosi każdy ze składników?
4. Na ogrodzenie kwadratowej działki zużyto 74 metry bieżących siatki. Szerokość furtki jest równa 2 m. Jakie wymiary ma ta działka?

Klasa 5

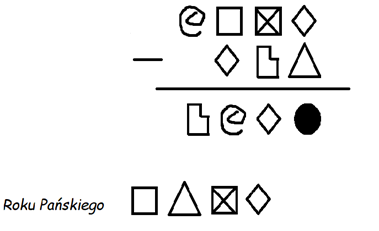
1. Obok przedstawione są zaszyfrowane rachunki z roku 1807. Rozszyfruj je.
   

1. Maszt wkopany w ziemię na 2/13 swojej długości wznosi się nad ziemię na wysokość 5 1/2 m. Oblicz długość masztu.
2. Adam miał wczoraj trzy oceny z matematyki i jego średnia ocen była równa 3,0. Oblicz, jaka ocenę dostał  Adam z klasówki, jeżeli ma teraz średnią równą 3,5.
3. 
   

– Mamo, ile waży ten posążek? – zapytał Piotr, wskazując na posążek Thotha, egipskiego boga mądrości, patrona matematyków.
– 3/4 kilograma i jeszcze 3/4posążka – odpowiedziała mama.

Ile kilogramów waży posążek?

Klasa 6

1. Ania dostaje 38 zł kieszonkowego, z czego 0,25 wydaje na słodycze. Jej koleżanka Ola przeznacza na słodycze 9,20 zł, co stanowi 0,25 jej kieszonkowego. Która z nich ma większe kieszonkowe? Która wydaje mniej na słodycze? O ile mniej?
2. Do sklepu sprowadzono z hurtowni 240kg masła, 150 kg cukru i 30 kg makaronu. Zakupione towary sprzedano w cenach: masło 2,00 zł za kostkę o wadze 250g, cukier 1,80 zł za kilogram, makaron 3,00 zł za 0,5 kg paczkę.
   a) Ile kosztowały wymienione towary w hurtowni, jeśli sprzedawca pobierał marżę stanowiącą 1/5 ceny hurtowej?
   b) Jaką kwotę zysku sprzedawca otrzymał za te artykuły?
3. Obwody dwóch prostokątnych działek są jednakowe i wynoszą po 120 metrów. Długość jednej z działek jest równa 40 metrów, a szerokość drugiej stanowi 0,8 szerokości pierwszej. O ile arów różnią się pola tych działek?
4. Wyznacz liczbę, której 1/4 wynosi:
   

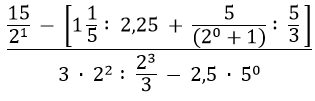
Klasa 7

1. Ojciec ma 45 lat, a jego synowie 10 i 8 lat. Po ilu latach ojciec będzie miał tyle lat, ile obaj synowie razem?
2. Mosiężny wałek został podzielony na trzy różnej wagi części. Na pierwszą z nich zużyto połowę wałka, na drugą 2/3 reszty. Masa trzeciej części była równa 3 kg. Jaka była masa całego wałka?
3. Ojciec i córka mają razem 62 lata. 4 lata temu ojciec był 8 razy starszy od córki. Ile lat ma obecnie każde z nich?
4. Suma dwóch liczb jest 2 razy większa od ich różnicy, przy czym pierwsza liczba jest o 2,6 mniejsza od drugiej. Wyznacz te liczby.

Klasa 8

1. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wartość wyrażenia 6 ¹⁰⁰ + 6 ¹⁰⁰ + 6 ¹⁰⁰ + 6 ¹⁰⁰ + 6 ¹⁰⁰ + 6 ¹⁰⁰ jest równa

A. 6 ⁶⁰⁰

B. 6 ¹⁰¹

C. 36¹⁰⁰

D. 36⁶⁰⁰

2. Wszystkich liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym nie występuje cyfra 2, jest

 A. 900

B. 729

C. 648

D. 512

3. Dla każdej liczby rzeczywistej 𝑎 wartość wyrażenia (3 + 4𝑎) ² − (3 − 4𝑎) ² jest równa

A. 32𝑎 ²

B. 0

C. 48𝑎

D. 8𝑎 ²

4. Wykaż, że dla każdej liczby całkowitej nieparzystej 𝒏 liczba 𝒏 ^𝟐 + 𝟐𝟎𝟐𝟑 jest podzielna przez 𝟖.

Rozwiązania

1.  B 6·6¹⁰⁰=6¹⁰¹

2. C  9·9·9=729

3. C Wskazówka – skorzystaj ze wzorów skróconego mnożenia lub zapisz potęgowanie za pomocą mnożenia (3 + 4𝑎) ²=(3 + 4𝑎) ·(3 + 4𝑎)

4. Niech 𝑛 będzie liczbą całkowitą nieparzystą. Wtedy 𝑛 = 2𝑘 + 1 przy pewnym 𝑘 całkowitym, więc   𝑛 ² + 2023 = (2𝑘 + 1) ² + 2023 = 4𝑘 ² + 4𝑘 + 1 + 2023 = 4𝑘(𝑘 + 1) + 2024. Jeżeli 𝑘 jest liczbą parzystą, to liczba 4𝑘(𝑘 + 1) jest podzielna przez 8 jako iloczyn liczby 4, liczby parzystej 𝑘 i liczby całkowitej 𝑘 + 1. Jeżeli 𝑘 jest liczbą nieparzystą, to liczba 4𝑘(𝑘 + 1) jest podzielna przez 8 jako iloczyn liczby 4, liczby parzystej 𝑘 + 1 i liczby całkowitej 𝑘. Liczba 2024 jest podzielna przez 8, gdyż 2024 = 8 ⋅ 253. Zatem liczba 4𝑘(𝑘 + 1) + 2024 jest podzielna przez 8 jako suma liczb podzielnych przez 8. To kończy dowód.

Luty

Klasa 4

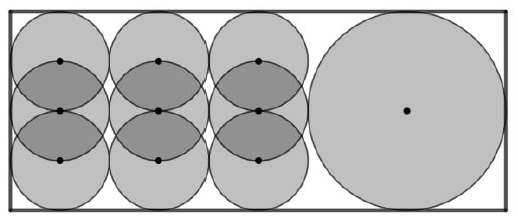
1. Każde z małych kół na rysunku ma promień równy 2 cm. Ile wynosi obwód prostokąta.
   

2. Asia, Kasia, Basia i Stasia to koleżanki z jednej klasy. Asia jest starsza od Basi o 36 dni, a Kasia starsza od Stasi o 47 dni, natomiast Stasia jest młodsza od Asi o 57 dni. Basia obchodzi urodziny 14 października. Kiedy obchodzi swoje urodziny Kasia?
3. W każdą kratkę wpisz inną cyfrę tak, aby działanie było poprawne:

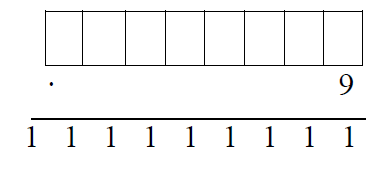
Klasa 5

1. Znajdź wszystkie liczby czterocyfrowe podzielne przez 18, w których cyfra jedności tysięcy jest równa 5, a cyfra dziesiątek jest równa 3.
2. Na jednej szalce wagi położono tabliczki czekolady, a na drugiej ⅖ takiej samej czekolady i 12 dekagramów. Nastąpiła równowaga. Ile ważyła tabliczka czekolady?
3. Ile to jest: dwie piąte z jednej trzeciej połowy?

Klasa 6

1. Dziewczęta z klasy VI postanowiły uporządkować plac szkolny w ciągu 6 godzin. Gdy wykonały &frac23 pracy, do pomocy zgłosiła się grupa dziewcząt stanowiąca 0,6 pracujących. W ciągu ilu godzin uporządkują pozostałą część placu, pracując z taką samą wydajnością?
2. Na koniec roku szkolnego średnia ocen w pewnej 28 – osobowej klasie wynosiła 4,25. Chłopców było o 4 mniej niż dziewcząt. Średnia ocen dziewcząt wynosiła 4,4. Jaka była średnia ocen chłopców?
3. W liczbie dwucyfrowej cyfra jedności jest o 6 większa od cyfry dziesiątek. Wyznacz różnicę między liczbą daną, a liczbą powstałą po przestawieniu jej cyfr.

Klasa 7

1. Oblicz wartość wyrażenia dla a=3,2 i b=0,5
   2[ 5a + 3( a – 2 )] – 4( 2a – b ) – 0,6
2. Napisz wyrażenie w najprostszej postaci:
   a – { 2a – [ 6a – ( 12a + 12 )]}
3. Wyłącz wspólny czynnik przed nawias i uprość wyrażenie bez wymnażania:
   3a( 2x – 1 ) + 6a( -3x+2)

Klasa 8

1. Oblicz pole powierzchni bocznej i objętość graniastosłupa prawidłowego czworokątnego o krawędzi podstawy 12cm i wysokości 20cm.
2. Trzy zeszyty i pięć ołówków kosztują razem 8,20 zł, natomiast trzy zeszyty i dziewięć ołówków 10,80 zł. Policz kolejno ile kosztują cztery ołówki, ile kosztuje jeden ołówek, ile kosztuje jeden zeszyt.
3. Paweł zamierzał kupić 4 porcje lodów, zabrakło mu jednak 80 groszy. Kupił więc 3 porcje, a wtedy pozostało mu 30 groszy. Jaka była cena jednej porcji lodów?

Styczeń

Klasa 4

1. Rodzina Edwarda podróżuje ze stałą prędkością i przejechała 400 kilometrów w ciągu 8 godzin. Ile czasu im zajmie przejechanie kolejnych 20 kilometrów?
2. Kielce mają 5 razy więcej mieszkańców niż Ciechanów. Warszawa ma 50 razy więcej mieszkańców niż Ciechanów. Ile razy więcej mieszkańców ma Warszawa niż  Kielce?
3. Heniek i Staszek zjeżdżali na nartach i korzystali z wyciągów narciarskich. Wyciąg Heńka kosztował 4 złote za podciągnięcie na górę, zaś wyciąg Staszka 3 złote za podciągnięcie na górę. Gdy chłopcy wracali do domu, okazało się, że każdy z nich wydał tyle samo pieniążków na wyciągi. Ile razy każdy z nich zjechał z góry na dół, jeśli wiadomo, że każdy z chłopców miał przy sobie 20 złotych.
4. Sześć dziewczynek uszyło 15 ubranek dla lalek w czasie jednego spotkania. Ile dziewczynek musi przyjść by w czasie jednego spotkania uszyły 25 ubranek dla lalek?

Klasa 5

1. Oblicz 0,15 liczby a, jeżeli:
   ( 12 × 0,6 – ⅖ ) × 5 + a = 47,5
2. Za 6 kg mąki i 3 kg cukru Ania zapłaciła 22,80 zł, a Ola za 3 kg takiej samej mąki i 3 kg cukru zapłaciła 15,60 zł. O ile zł różni się cena 1 kg mąki i 1 kg cukru?
3. Magda jest o 2 lata starsza od siostry i o 3 lata młodsza od brata. Razem mają 37 lat. Ile lat ma każde z nich? Ile lat mają rodzice Magdy, jeżeli jest ona 3 razy młodsza od mamy, a mama jest o 3 lata młodsza od taty?
4. O ile należy zmienić wartość wyrażenia
   94 ⅕ : 3 – ( 1 + 2 ⅓ ) × 3
   aby otrzymać liczbę dwucyfrową podzielną przez 25? Ile jest takich liczb? Rozpatrz wszystkie przypadki.

Klasa 6

1. Ola zebrała 50 kg porzeczek, które umieściła w trzech jednakowych skrzynkach. Waga pustej skrzynki wyniosła 1 ⅓ kg. Pierwsza skrzynka ważyła brutto 16 kg 75 dag, a druga 16,6 kg. W której skrzynce było najmniej porzeczek, a w której najwięcej?
2. Dwulitrowa butelka napoju kosztuje 3 ⅕ zł, a półtoralitrowa butelka tego samego napoju kosztuje 2 ⅘ zł. Ile pieniędzy zaoszczędzisz, kupując 24 litry napoju tańszego?
3. Kasia obliczyła, że jeżeli będzie szła z prędkością 50 m/min, to dojdzie do szkoły w ciągu 30 minut. Po przejściu ⅔ drogi zatrzymała się na 5 minut. Z jaką prędkością musi iść dalej, aby dojść do szkoły w zaplanowanym czasie?
4. W trójkącie miara jednego kąta stanowi ⅔ miary drugiego kąta. Jeżeli miarę kąta trzeciego zmniejszymy 64%, a miarę kąta pierwszego zwiększymy o 48^o, to otrzymamy trójkąt prostokątny. Oblicz miary kątów tych trójkątów.

Klasa 7

1. Uzasadnij, że jeśli liczba jest podzielna przez 15 i przez 14, to jest podzielna przez 10.
2. Za przejazd autostradą Karol zapłacił 8,4 euro. Potem powiedział, że płacił tylko monetami o nominałach 0,20 euro i 0,50 euro i że monet tych było 20. Czy może to być prawda? Odpowiedź uzasadnij.
3. Zapisano trzy różne liczby, których średnia arytmetyczna jest równa 4, oraz dwie inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 3,2. Zapisz obliczenia.
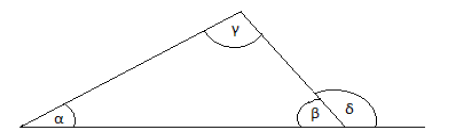
4. Kąty wewnętrzne trójkąta mają miary α, β i γ, a kąt przyległy do kąta o mierze β ma miarę δ (rysunek poniżej). Wykaż, że δ = α + γ.

Klasa 8

Grudzień

Klasa 4

1. Zbliżające się Święto to czas wytężonej pracy dla Mikołaja. Do pomocy poprosił zaprzyjaźnionych Mikołajów. Jeśli 9 Mikołajów rozdaje w 30 minut 60 prezentów to ile prezentów rozda 36 Mikołajów w 3 godziny?
2. Mikołaj z żoną postanowili wydać małe przyjęcie w ogrodzie. Zaprosili na nie 9 par królewskich, każdej towarzyszyły po 3 damy dworu, 7 ambasadorów z żonami i grupę artystów cyrkowych. Obecnych było 85 osób. Jak liczna była grupa cyrkowców?
3. Mikołaj miał 54 prezenty dla dzieci z czego 5 prezentów opakowanych w niebieski papier, 10 w fioletowy, a reszta w czerwony. Oblicz ile prezentów było opakowanych w papier czerwony. O ile więcej prezentów było opakowanych w papier czerwony niż w papier fioletowy i niebieski razem.
4. Dzień 1 grudnia pewnego roku wypadł w piątek. W jaki dzień tygodnia obchodzono wówczas Boże Narodzenie?

Klasa 5

1. Renifery Mikołaja przebywały na podwórku, które miało kształt prostokąta. Było długie na 516 metrów i szerokie na 320 metrów. Pewnego dnia Mikołaj wydał zarządzenie, aby skrzaty zrobiły nowe ogrodzenie. Ile metrów nowego ogrodzenia muszą zrobić skrzaty?
2. Po przyjęciu Mikołajowa poleciła skrzatowi, aby obliczył, ile kosztowało wydanie przyjęcia. Okazało się, że goście wypili 25 litrów soku pomarańczowego w cenie 3 zł za litr, zjedli 12 kg winogron w cenie 5 zł za kilogram, 9 kg pomarańczy w cenie 4 zł za kilogram i 8 kg różnych ciast w cenie 14 zł za kilogram. Skrzat oświadczył, że wydanie przyjęcia kosztowało 273 złote. Sprawdź, czy skrzat dobrze wykonał obliczenia. Jeśli pomylił się to podaj o ile zł.
3. Na choince wisi 20 bombek, 15 aniołków i 3 łańcuchy. Niestety, gdy Jasio otworzył drzwi zbiło się  1/2  bombek i o 5 mniej aniołków niż bombek. Ile ozdób pozostało na choince?
4. Na choince wisiało 26 cukierków. Grzesiek zawiesił jeszcze 3 razy więcej cukierków. Po chwili przyszła Gabrysia i zjadła 12 cukierków. Ile cukierków pozostało na choince?

Klasa 6

1. Święty Mikołaj przygotował paczki dla dzieci. Ma 180 cukierków, 150 pierników i 60 lizaków. Chce je podzielić tak, aby każde dziecko dostało po tyle samo słodyczy każdego rodzaju. Ilu dzieciom może przygotować w ten sposób paczki?  Po ile słodyczy każdego rodzaju dostanie każde dziecko? Podaj wszystkie możliwe rozwiązania.
2. Zuza ma urodziny w mikołajki. Napisała list do św. Mikołaja i zapytała, ile ma on lat. List schowała pod poduszkę, a następnego dnia znalazła tam odpowiedź: „Mam tyle lat, ile Ty liczysz sobie miesięcy”. Zuza pomyślała chwilę i wykrzyknęła: „To razem mamy 91 lat!”. Ile lat ma Zuza?
3. Aneta i Wojtek robią listę świątecznych dań. Na początku wpisali 6 potraw. Potem Wojtek wykreślił jedną, bo jej nie lubi, a Aneta za to dopisała barszcz i kompot z suszu. Wtedy Wojtek przypomniał sobie o rybach i dopisał 3 potrawy, jednak Aneta jedną z nich wykreśliła. Potem przyszła mama i dopisała jedną potrawę i na koniec tata dopisał jeszcze dwie. Ile potraw będzie na stole wigilijnym u Anety i Wojtka?
4. Dzieci wieszają na choince ozdoby w kolejności: najpierw miś, potem bałwan, skarpeta, znowu bałwan, sowa i znowu … Powiesiły w ten sposób 20 ozdób. Ile powiesiły misiów, ile bałwanów, ile skarpet, ile sówek? Jakich ozdób jest na choince najwięcej?

Klasa 7

1. Pewien Mikołaj niósł z miasta A do miasta B ciężki wór z prezentami. Gdy był dokładnie w połowie drogi, spotkał zaprzęg reniferów, który zabrał go do miasta B. Po rozdaniu wszystkich prezentów Mikołaj wrócił pieszo do miasta A. W którą stronę podróżował dłużej, jeśli z pustym workiem szedł dwa razy szybciej niż z pełnym?
2. W 2111 roku Mikołaj Starszy będzie miał 345 lat, a jego syn Mikołaj Młodszy 111 lat. W którym roku Mikołaj Starszy będzie dwa razy starszy od Mikołaja Młodszego.
3. Jest czwartek 14 grudnia godz. 7:55. Ile jeszcze czasu do Wieczerzy Wigilijnej, która odbędzie się 24 grudnia o godz. 16:30. Odpowiedź wyraź w dniach, godzinach i minutach oraz w godzinach i minutach.
4. Mikołaj Bardzo lubi geometrię. Ostatnio zauważył, że dwóch miastach w Polsce znajdują się bardzo podobne dachy. Na jednym z nich po przejściu 4 m, musi on skręcić w lewo o 53 stopnie, a następnie przejść jeszcze 5 m. Na drugim skręca po kolei o 43, 53 i 84 stopnie, przy czym ostatni odcinek drogi ma długość 6 m. Czy te dachy są przystające?

Klasa 8

1. Święty Mikołaj w tym roku ma wyjątkowo duży brzuch.  Jaką średnicę ma brzuch Mikołaja, wiedząc, że promień jest 16 razy mniejszy od liczby, której cyfrą setek jest 3, cyfra dziesiątek jest o 3 mniejsza od cyfry setek, a cyfra jedności jest ilorazem liczb 44 i 11.
2. W szkółce rosło 2000 drzewek. 40% stanowiły ozdobne drzewka liściaste, 20% to iglaki, a reszta to choinki, które zostaną wycięte na święta. Każda choinka kosztuje 50 zł, ile zarobi właściciel szkółki, jeśli sprzeda wszystkie drzewka?
3. Elfy urządziły wyścig reniferowymi zaprzęgami. Ailios jechał z prędkością 48 km/h, a Ainairos z prędkością 800 m/min. Który z elfów dotarł do mety szybciej, jeśli do pokonania mieli odcinek 24 000 m.
4. Święty Mikołaj ma w szufladzie 29 skarpetek: 9 niebieskich, 8 zielonych i 12 czerwonych. Wskutek zawiei śnieżnej gaśnie światło. Ile skarpetek Święty Mikołaj będzie musiał wyjąć, żeby na pewno mieć przynajmniej po jednej parze każdego koloru?

Listopad

Klasa 4

1. Agata, Bartek, Czarek i Diana zbierali kasztany. Kiedy Agata przełożyła do koszyka Bartka 15 kasztanów, a Bartek przełożył 12 kasztanów do koszyka Czarka, ten zaś 9 kasztanów dał Dianie, która 5 kasztanów oddała Agacie, to okazało się, że wszyscy mają po 36 kasztanów. Oblicz, ile początkowo kasztanów miało każde dziecko. Zapisz obliczenia i podaj odpowiedź.
2. Światła sygnalizacyjne na pewnym skrzyżowaniu zmieniają się w następujący sposób: czerwone trwa 80 sekund, żółte – 5 sekund, zielone – 90 sekund, żółte – 5 sekund, znowu czerwone, żółte, itd. Ile czasu, w ciągu godziny, pali się zielone światło? Zapisz obliczenia i podaj odpowiedź.
3. Kasia kupiła 2 jogurty, 3 batoniki i 1 soczek i zapłaciła 17 złotych, a Bartek za takie same 3 jogurty, 2 batoniki i 4 soczki zapłacił o 11 złotych więcej. Ile reszty z 50 złotych otrzyma Julka jeśli kupi takie same 3 jogurty, 3 batoniki i 3 soczki? Zapisz obliczenia i podaj odpowiedź.
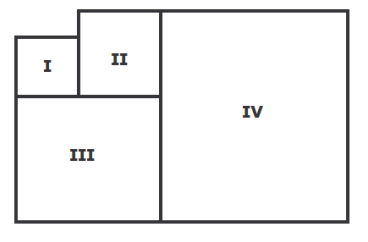
4. Figury I, II, III, IV są kwadratami. Obwód kwadratu I jest równy 16 m, a obwód kwadratu II jest równy 24 m. Oblicz obwód kwadratu IV. Zapisz obliczenia i podaj odpowiedź.

Klasa 5

1. Mały Kuba miał 255 klocków w skrzyni. Postanowił budować wieżę według zasady: I wieżę z 3 klocków, II wieżę z 5 klocków, III wieżę z 7 klocków, itd. Z ilu klocków zbudował przedostatnią wieżę?
2. Maciek rozwiązał równanie [ 18 + 12 : ( 12 – 2 * x )] : 4 = 6  i  otrzymał wynik x = 6. Sprawdź, czy te wynik jest poprawny. Jeśli nie, podaj prawidłowe rozwiązanie.
3. Ze śródziemnomorskiego portu wypłynęły jednocześnie dwa statki wycieczkowy (z ekipą nurków) i kuter rybacki. Oba płynęły w tym samym kierunku na odległą wyspę. Statek pasażerski płynął z prędkością 24 km/h a kuter z prędkością 15 km/h. Po 3 godz. rejsu statek wycieczkowy zatrzymał się na morzu (wtedy nurkowie oglądali świat podwodny). Potem statek ruszył w dalszą podróż  i po 7 godzinach dogonił kuter rybacki. Ile godzin trwała przerwa w rejsie statku wycieczkowego?
4. Ala pomalowała niebieską farbą drewnianą kostkę sześcienną o boku 9cm. Zużyła ¾ pojemnika farby o pojemności 50ml. Po pewnym czasie poprosiła o pocięcie tej kostki na małe kostki sześcienne o boku 3cm. Ile farby potrzebuje na pomalowanie na niebiesko pozostałych niepomalowanych ścian małych kostek ? Ile takich samych pojemników farby musi dokupić, aby wystarczyło na pomalowanie tych kostek?

Klasa 6

1. Pewien arbuz jest o 3kg cięższy od 1/3 arbuza. Ile waży ten arbuz?
2. Który z wielokątów ma 14 przekątnych?
3. Adam miał wczoraj trzy oceny z matematyki i średnią 3,0. Jaką ocenę dostał dzisiaj, jeśli teraz jego średnia wynosi 3,5?
4. W pudełku jest 30 kul: białe, czerwone i niebieskie. Kul niebieskich jest 9 razy mniej niż kul czerwonych. Ile jest kul każdego koloru w tym pudełku? Odpowiedź uzasadnij. Rozpatrz wszystkie możliwe przypadki.

Klasa 7

1. Trzy gitary kosztują razem 2250 zł. Cena jednej stanowi 2/3 ceny drugiej gitary, a trzecia ½ średniej arytmetycznej ceny pierwszej i drugiej. Oblicz cenę każdej z trzech gitar.
2. Cenę towaru podniesiono o 100%. O ile procent trzeba obniżyć tę nową cenę, aby wróciła do poprzedniego poziomu? Cenę innego towaru podniesiono o 25%. O ile procent trzeba ją zmniejszyć, aby była taka sama jak przed podwyżką?
3. „Koszmarny sen szewca”. W pewnym mieście mieszka 20 000 ludzi. Pięć procent z nich jest jednonogich, a połowa pozostałych chodzi boso. Ile butów noszą w sumie mieszkańcy tego miasta?
4. W kryptogramie różnym literom odpowiadają różne cyfry. Podaj rozwiązanie, w którym liczba „SZEŚĆ” jest największa z możliwych.

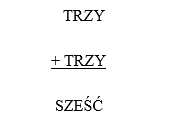
Klasa 8

1. Liczba 390 jest sumą kwadratów trzech różnych liczb pierwszych. Znajdź te liczby.
2. Używając jedynie cyfr 3 i 7 (każdej przynajmniej raz), zapisz liczbę dającą przy dzieleniu przez 3 taką samą resztę, jak przy dzieleniu przez 7.
3. Czy używając jedynie cyfr 3 i 7 (każdej przynajmniej raz), można zapisać liczbę dającą przy dzieleniu przez 13 i 31 taką samą resztę?
4. Jeśli w liczbie 2003 zastąpimy pierwsze albo drugie zero cyfrą 5, to otrzymamy dwie liczby pierwsze 2503 i 2053. Czy oprócz piątki jakaś inna cyfra ma taką własność?

Październik

Klasa 4

1. Dziesięciu uczestników konkursu otrzyma nagrody. Jaka będzie łączna suma nagród, jeśli wiadomo, że kolejny uczestnik otrzyma 500 zł mniej niż ten, który wyprzedził go w punktacji, zaś ostatni dostanie 100 zł? Zapisz wszystkie obliczenia i podaj odpowiedź.
2. Agata w swoim gospodarstwie domowym posiada 30 owiec, pewną liczbę gęsi i nie posiada żadnych innych zwierząt. Liczba nóg wszystkich gęsi jest równa liczbie nóg wszystkich owiec. Ile zwierząt posiada Agata w swoim gospodarstwie? Zapisz wszystkie obliczenia i podaj odpowiedź.
3. Ania, Beata, Celina i Dorota wybrały się na grzyby. Ania zebrała trzy razy więcej grzybów od Beaty, Beata trzy razy więcej od Celiny, a Celina trzy razy więcej od Doroty. Wiadomo, że razem mają więcej niż 50 , ale mniej niż 100 grzybów. Ile grzybów ma każda z dziewczynek? Zapisz wszystkie obliczenia i podaj odpowiedź.
4. Na poniższych rysunkach znajdują się działania ułożone przy użyciu zapałek. Przełóż tylko jedną zapałkę, tak by otrzymać prawdziwą równość

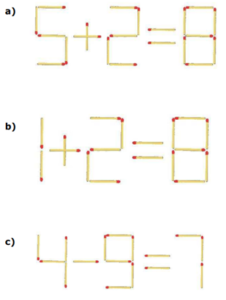
Klasa 5

1. W trzech koszach było razem 210 jabłek. Gdyby z pierwszego kosza przełożyć 6 jabłek do drugiego, a z drugiego – 16 do trzeciego, to w każdym koszu byłoby tyle samo jabłek. Ile jabłek było w każdym koszu?
2. Suma trzech liczb jest równa 167. Różnica pierwszej i drugiej wynosi 23, a różnica drugiej i trzeciej liczby jest równa 24. Czy prawdą jest, że trzecia liczba jest najmniejsza, a pierwsza największa? Wyznacz liczbę najmniejszą.
3. Cyfry dowolnej liczby trzycyfrowej są kolejnymi malejącymi liczbami naturalnymi. Oblicz różnice między dowolnie w ten sposób utworzoną liczbą a liczbą, utworzoną z cyfr zapisanych w odwrotnej kolejności. Rozważ wszystkie przypadki. Czy zauważyłeś jakąś prawidłowość?
4. Suma trzech liczb jest równa 81,6. Środkowa liczba jest ich średnią  arytmetyczną i stanowi 0,8 największej liczby. Wyznacz najmniejszą liczbę.

Klasa 6

1. Rodzice Jasia mają w sumie 69 lat. 30 lat temu tata Jasia był dwa lata starszy od swojej przyszłej żony. Ile lat mają rodzice Jasia?
2. Średnia arytmetyczna trzech dodatnich liczb naturalnych jest mniejsza niż 2⅔. Jedna z tych liczb jest sumą pozostałych. Znajdź te liczby.
3. W hurtowni znajduje się herbata w paczkach po 16 kg, 17 kg i 40 kg. Czy można kupić 100 kg herbaty bez rozpakowywania paczek?
4. Prostokątny trawnik ma wymiary 30 m x 25 m. Poprowadzono przez trawnik ścieżkę (jak na rysunku) i wysypano żwirem na grubość 5 cm. Ile m³ żwiru wysypano?

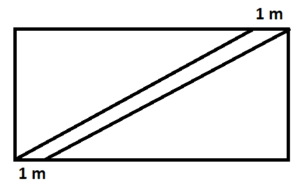
Klasa 7

1. Na pytanie, ile ma lat, Olek odpowiada: „Mój obecny wiek i wiek mojego ojca są liczbami lustrzanymi, a w ubiegłym roku mój wiek i wiek mojej mamy wyrażały się również liczbami lustrzanymi. Moi rodzice mają razem 93 lata”. Ile lat ma obecnie Olek?
2. W pewnej publicznej szkole podstawowej 65% uczniów uczy się języka angielskiego, a 78% uczy się niemieckiego. Jaki procent uczniów uczy się obu języków, jeżeli zakładamy, że każdy uczeń uczy się przynajmniej jednego języka? Ilu uczniów jest w tej szkole, jeżeli wiadomo, że obu języków uczy się 172 uczniów? Ilu uczy się tylko języka angielskiego, a ilu tylko niemieckiego?
3. Uzasadnij, że jeśli od liczby trzycyfrowej odejmiemy sumę jej cyfr, to otrzymany wynik jest podzielny przez 3.
4. Wojtek chce zapisać na płycie CD-ROM zdjęcia, z których każde ma rozmiar 560 KB. Obliczył, że na płycie zmieści się 1250 zdjęć. Ile zdjęć mógłby zapisać na tej płycie, jeśli byłyby one lepszej jakości i każde z nich zajmowałoby 1,4 MB pamięci? (Przyjmij, że 1 megabajt MB= 1000 kilobajtów KB).

Klasa 8

1. Wykaż, że wśród liczb czterocyfrowych ponad 70% to liczby złożone.
2. Pewna liczba ma 4 dzielniki, których średnia arytmetyczna jest równa 10. Znajdź tę liczbę.
3. Znajdź wszystkie liczby dwucyfrowe, które przy dzieleniu przez 7 dają taką samą resztę jak przy dzieleniu przez 13.
4. Wojtek miał trzy patyczki: czerwony, zielony i niebieski. Ich długości to: 2cm, 3cm, 5 cm (kolejność liczb nie odpowiada podanej kolejności kolorów). Za pomocą każdego patyczka Wojtek mierzył długość krawędzi stołu. Zielony zmieścił się 75 razy, niebieski 50 razy. Czerwony zmieścił się także całkowitą liczbę razy – ile?